
• The process of finding non-periodic tiling schemes and associated tiles is like breaking a vase and restoring it. However, the researchers hope that the fragments formed after the vase shattered are uniform, and that the broken texture is "aperiodic". Even if such tiles are spread all over the world, the mosaic pattern will not repeat.

Terence Tao, a Chinese mathematician, Fields Medal winner, and professor of the Department of Mathematics at the University of California, Los Angeles
Is it possible to find a tile that will never repeat its pattern even if it is used to cover the whole world?
Recently, Terence Tao, the "Mozart" in the mathematics world, a Chinese mathematician, Fields Medal winner, and professor of the Department of Mathematics at UCLA, announced on his personal blog that he overturned the "periodic tiling conjecture".
They found one such "tile" in ultrahigh-dimensional space.
According to the preprint website arXiv, related papers co-authored by Terence Tao and his collaborators were uploaded in the early morning of November 29, 2022.
But in fact, Tao Terence announced the above news on his blog more than two months in advance; and in the early morning of September 18, they submitted an abbreviated "announcement" paper to the arXiv website—announcement, the full text of which is 13 pages.
The full version of the dissertation has 48 pages. The title of the paper is "A counterexample to the periodic tiling conjecture".
The co-author of the paper is Rachel Greenfeld, former assistant professor of Hedrick, Department of Mathematics, UCLA, and now member of the School of Mathematics of the Institute for Advanced Study in Princeton, USA. She is a postdoctoral fellow of Terence Tao.
The Nobel Prize and the Puzzle That Never Repeats
What is the periodic tiling conjecture?
It seems that it is not difficult to imagine using square tiles of the same size to cover the floor of a square room. People only need to tile tiles of appropriate size without leaving any gaps like "copy and paste". On such a floor, the periodicity of the pattern is obvious: if you translate part of the pattern to another location, it's as if it hadn't been moved.
This is perhaps one of the easiest "construction schemes" known as periodic tiling.

Different effects produced by periodic tiling and non-periodic tiling. Screenshot from "Aperiodic Texture Mapping"
Six years ago, on February 18, 2016, mathematician Siddhartha Bhattacharya (Siddhartha Bhattacharya), a mathematician from the School of Mathematics of the Tata Institute of Fundamental Research, Mumbai, India, uploaded a preprinted paper "Periodicity and decidability of tilings" on the arXiv website. of ℤ^2", announced that it proved the "periodic tiling conjecture" on the two-dimensional plane - through translation, a single tile can only be tiled periodically on the plane, and cannot be tiled aperiodically.
Mathematicians speculate that in higher dimensions beyond two dimensions, there is no tile that can be tiled aperiodically with the same type. This assumption is known as the "periodic tiling conjecture".
In other words, the "periodic tiling conjecture" asserts that if only translation can be used to tile or fill, then in any dimension (two-dimensional and above), there is no piece that can tile the entire Surface or special tiles that fill the entire space. Even if such a tile is designed, it can only tile or fill the corresponding space in a periodic manner.
But the "periodic tiling conjecture" seems to hold true only on a two-dimensional plane.
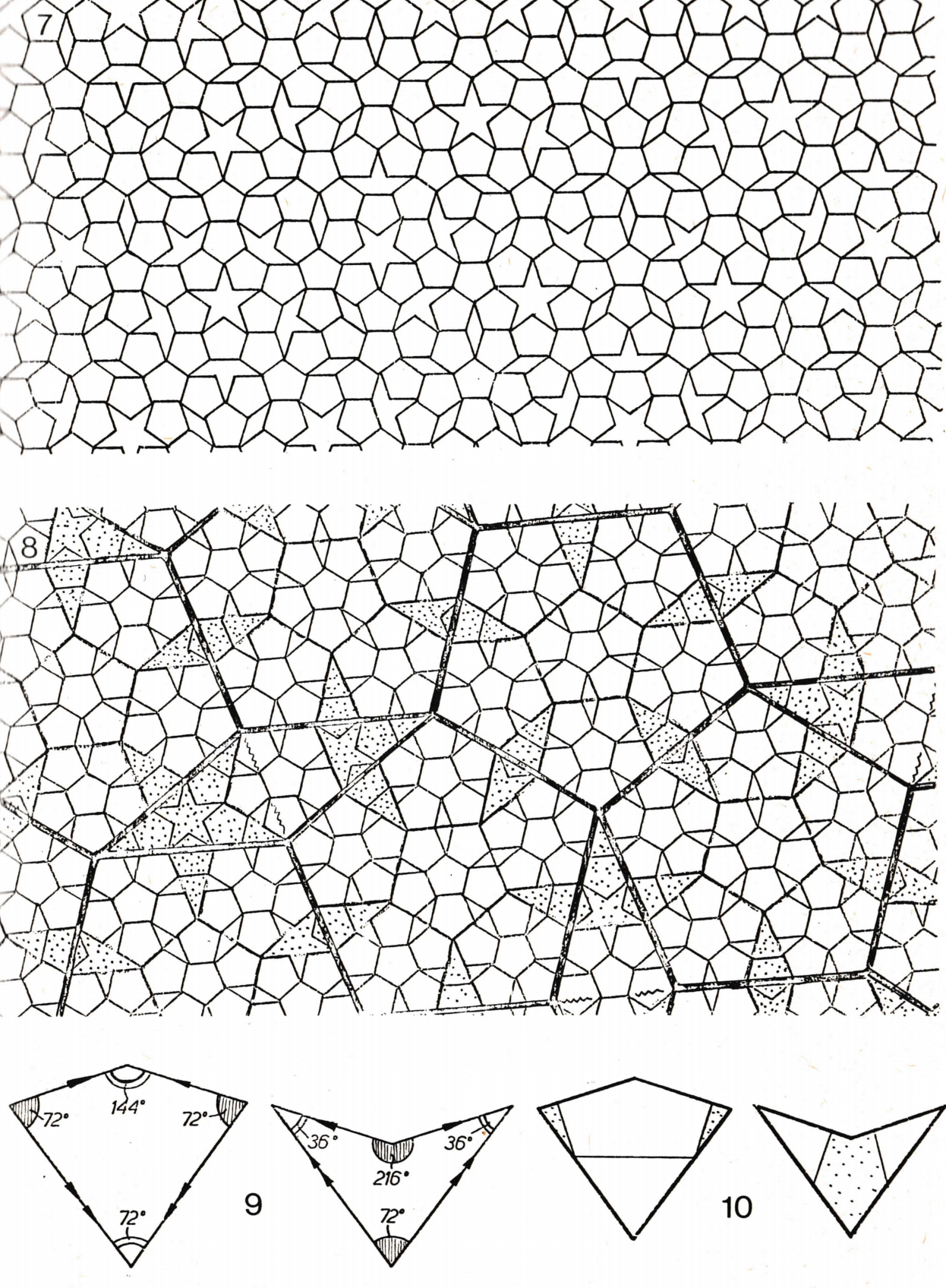
One of the Penrose tile styles. Screenshot from Eureka 39(1978) 16-32
As early as sixty years ago, around 1960, Wang Hao, a Chinese mathematician who taught at Oxford University, studied the periodic tiling problem during his academic visit to Bell Telephone Laboratories in New Jersey, USA, and proposed the "Wang Brick" (or Wang bricks, Wang Hao tiles, aka Wang squares) model.

Partial Wang Hao tile. From Parcly Taxel
Four years later, a seemingly more advanced solution emerged: aperiodic tiling. Although it is also a lot of tiles spliced together, densely covering the entire floor, but the splicing pattern will never repeat, even if the entire world is covered. In 1964, Wang Hao's student Robert Berger proposed the earliest aperiodic tiling scheme, which required 20426 tile combinations.
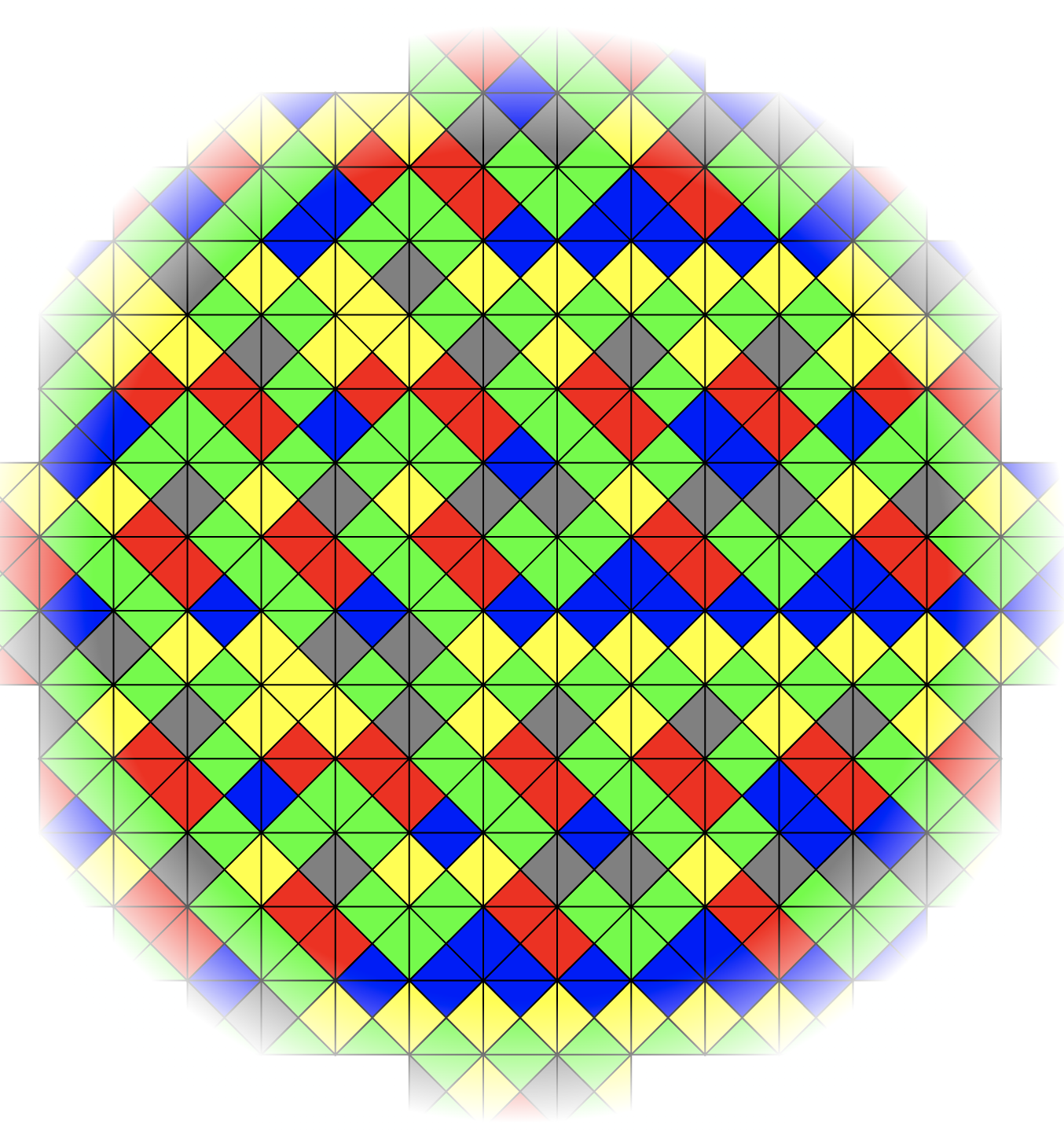
A non-periodic tiling with "king bricks". By Claudio Rocchini
Subsequently, Roger Penrose, a British mathematical physicist and honorary professor of the Department of Mathematics at Oxford University, reduced the required tile combinations to 5, and finally only used 2 types of tile combinations, such as one large and one small two A rhombus can realize aperiodic tiling on a two-dimensional plane. Such tiles are known as Penrose tiles. It became one of the symbols of mathematical art and was spread on the floors of buildings related to famous universities such as the Department of Mathematics of Oxford University. The related tiling style is known as Penrose tiling, or Penrose tessellation, Penrose tessellation, Penrose puzzle, Penrose geometric puzzle, etc.
Aperiodic patterns on a flat surface have a curious property in that information about their placement seems to be somehow transmitted across large distances, preventing certain tiles from appearing hundreds (or even thousands, millions) of tiles away. type of arrangement. Edmund Harriss, an assistant professor at the University of Arkansas, was the subject of his doctoral dissertation on Penrose tiling. "Local constraints sprang into global constraints sporadically," he said.
Penrose tiles are not only well-known in the mathematics world, but also in the field of architectural decoration and even in the field of material science, bringing new inspiration to people.
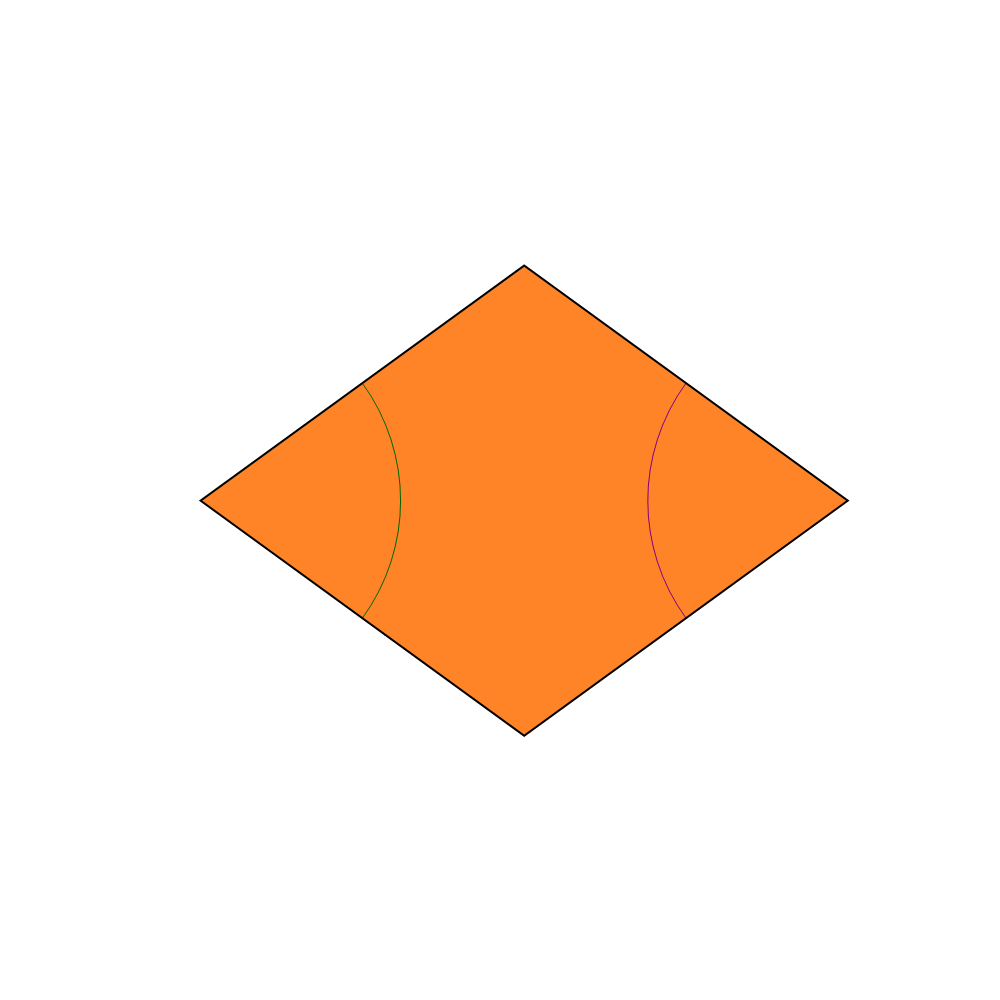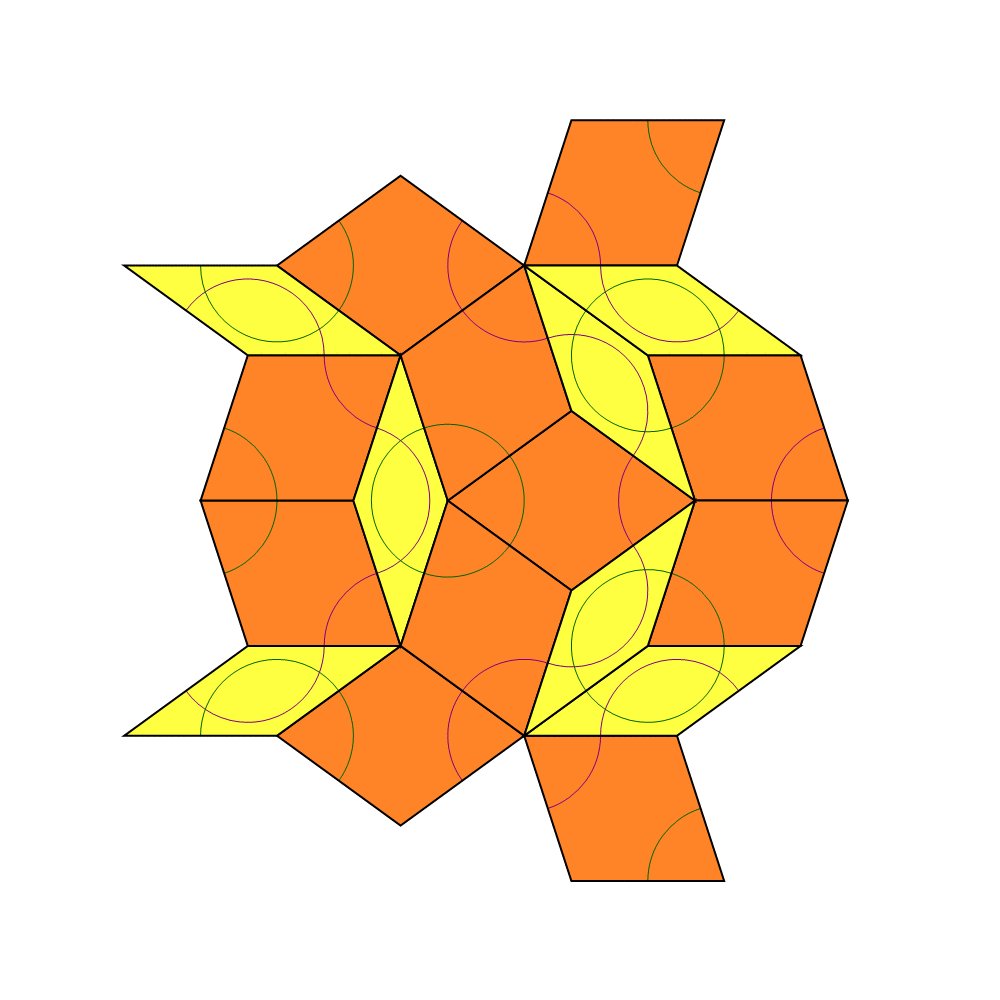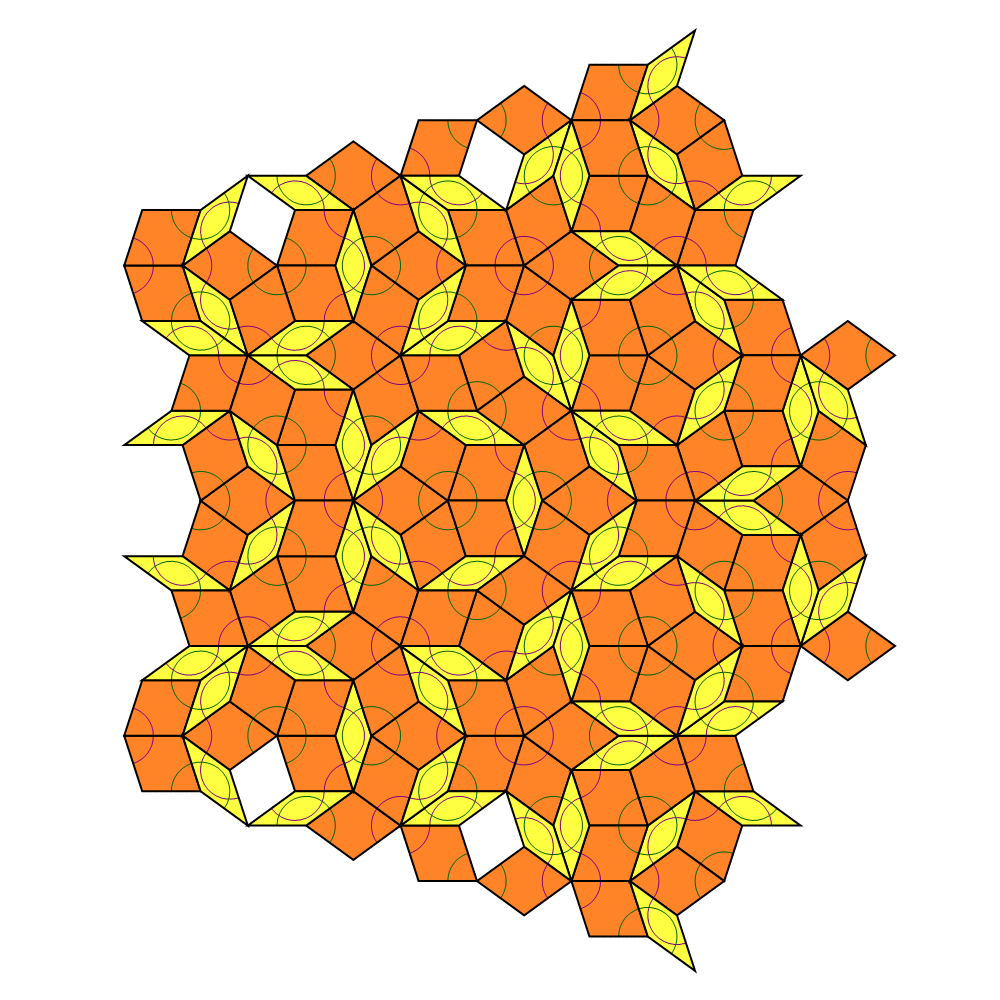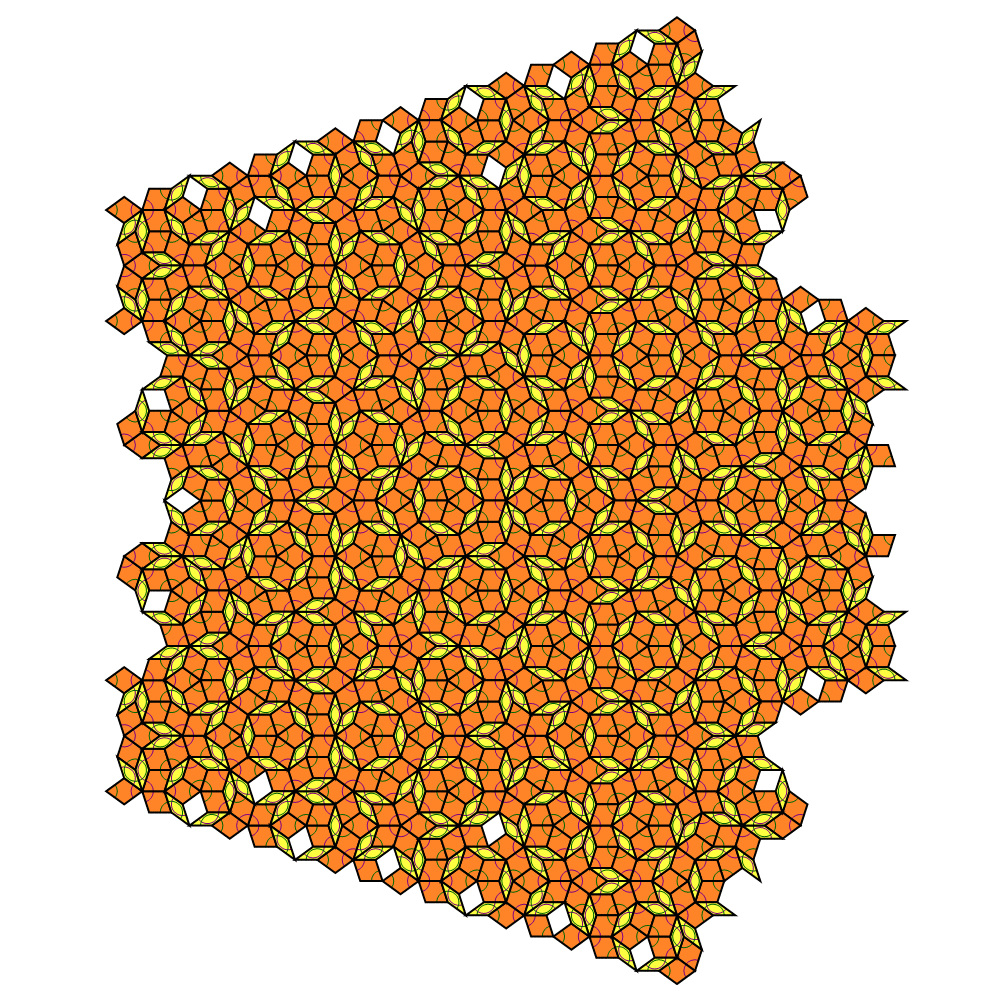
One of the styles of Penrose tiles or puzzles. from Taktaal
In 1982, Israeli materials scientist Dan Shechtman (Dan Shechtman), who was on an academic sabbatical in the United States, observed a strange diffraction pattern of the alloy in the laboratory, which did not conform to the previous impressions of crystals and lacked standard symmetry. The arrangement of their atoms is non-repetitive and non-periodic, just like the pattern of Penrose floor tiles. He later called it "quasicrystal".
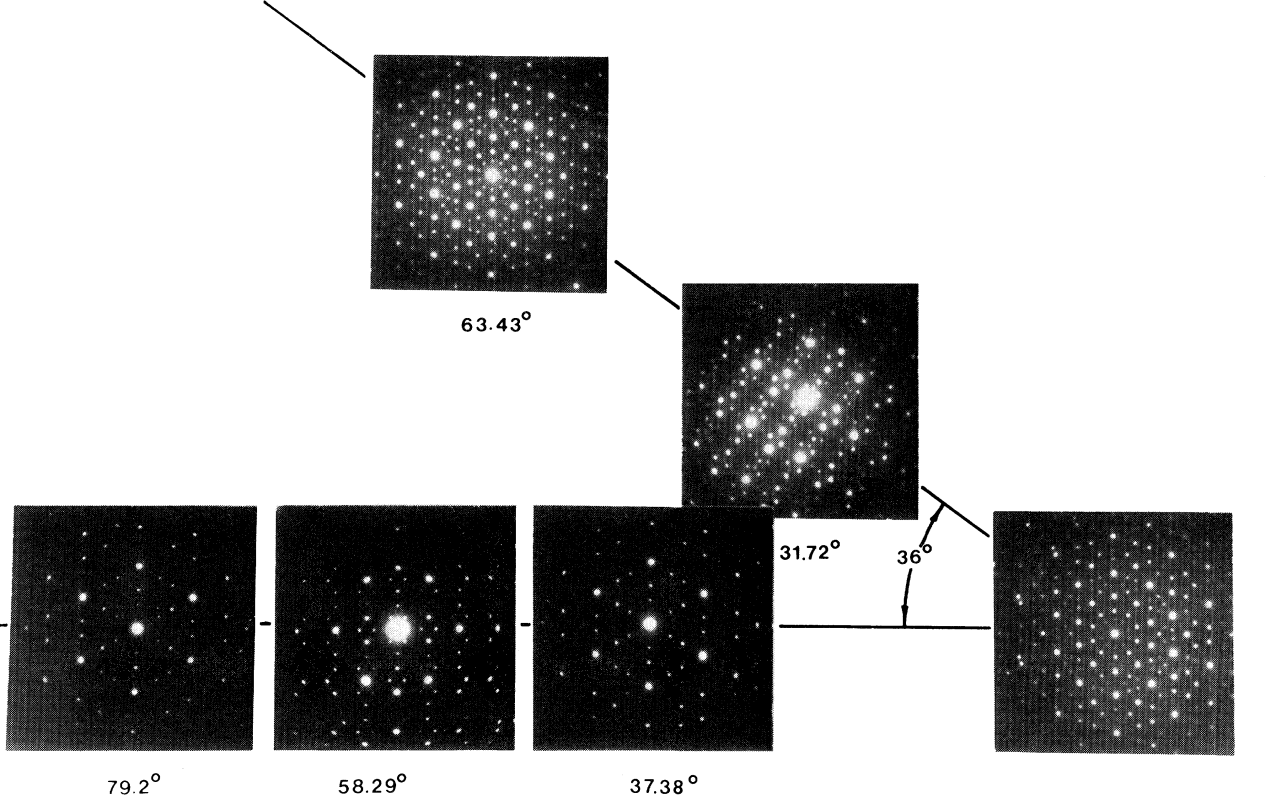
Electron diffraction image by Dan Shetman. Screenshot from Phys. Rev. Lett. Vol. 53(20), 1984
Dan Shetman's paper and his findings have generated a great deal of controversy and attack. Until more than 20 years later, in 2011, he was awarded the Nobel Prize in Chemistry for his "discovery of quasicrystals".

Electron diffraction picture of a quasicrystal. via nobelprize.org
In addition, Penrose is also one of the Nobel Prize winners.
On January 18, 1965, Penrose published a paper in Physical Review Letters, explaining Penrose's singularity theorem. After studying singularities with Penrose, Stephen Hawking overturned theories about the origin of the universe with Penrose's theorem. The singularity came to be known as a "black hole".
In 2020, 89-year-old Penrose was awarded the Nobel Prize in Physics for his "discovery that the formation of black holes is a powerful prediction of general relativity". He exclusively enjoys half of the prize, sharing it with German scientist Reinhard Genzel and American scientist Andrea Ghez who "discovered a supermassive compact object in the center of the Milky Way" won the 2020 Nobel Prize in Physics.
But the problem is that no one has ever completed the aperiodic tiling "game" with one tile. Until recently, Terence Tao and his collaborators found such a strange "tile" in ultra-high-dimensional space.
Find a counterexample with Sudoku and Tetris games
The process of finding non-periodic tiling schemes and related tiles is like breaking a vase and restoring it. However, the researchers hope that the fragments formed after the vase shattered are uniform, and that the broken texture is "aperiodic".
From "puzzles" on a two-dimensional plane to "stacking blocks" in a higher-dimensional space, Terence Tao hopes to find a single "tile" that can be stacked aperiodically.
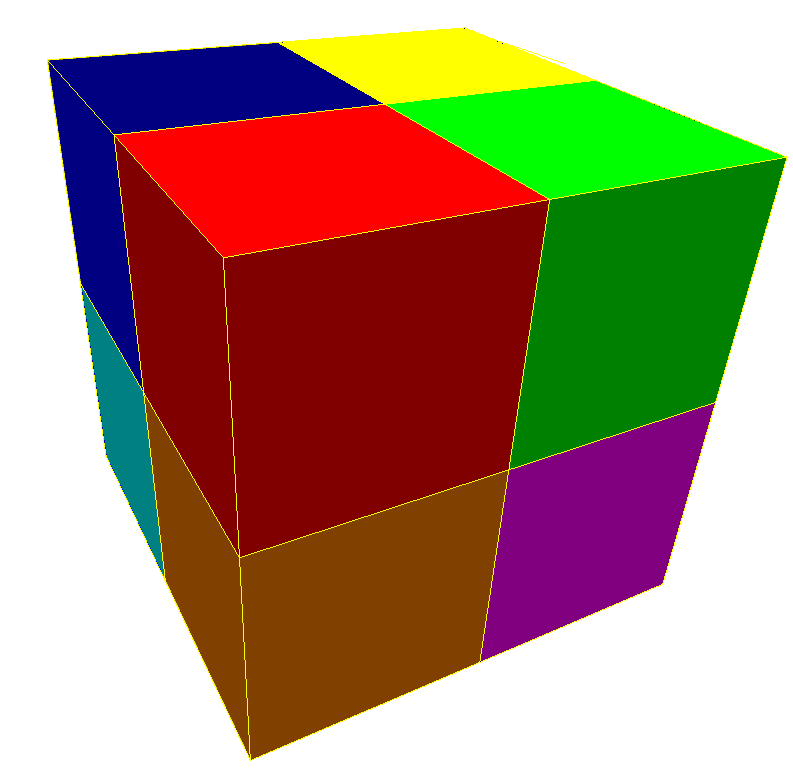
Cubic dense paving. by Tomruen
In a blog post explaining his latest proof strategy and methodology, Tao mentioned the games of Sudoku and Tetris, as well as computer programming.
Greenfield came to UCLA in 2019 as a postdoctoral fellow, three years after the Indian mathematician Siddhartha Bhattacharya proved the "periodic tiling conjecture" to hold on a two-dimensional plane. Later, she and Tao Terence used another method different from Siddhartha Bhattacharya to prove the "periodic tiling conjecture" in the two-dimensional plane again. However, when they wanted to advance to prove this conjecture in three-dimensional space, they hit a wall.
Tao Zhexuan said that there may be a reason why this conjecture cannot be proven in a higher dimension, and we should start looking for counterexamples.
In August 2021, they came close to their goal for the first time: They found two tiles in ultrahigh-dimensional space that could achieve aperiodic filling, but not one.
On August 17, 2021, Greenfield uploaded a paper co-signed by her and Tao Terence on the arXiv website, titled "Undecidable translational tilings with only two tiles, or one nonabelian tile". Six days later, she uploaded an updated version.
"Two is pretty close, but not enough," Greenfield said.

Match lines like a "Tetris game". Screenshot from Terence Tao's blog post on September 19, 2022
On September 19, 2022, Terence Tao stated in his blog post, "Greenfield and I have just uploaded our announcement, the 'Counterexample to the Periodic Tiling Conjecture', to arXiv. Announcement of a longer paper in a few weeks. In it, we disprove the periodic tiling conjecture of Grünbaum-Shephard and Lagarias-Wang."
In the aforementioned blog post, Terence Tao wrote that they created a "tiling language" that uses systems of tiling equations to describe non-periodic functions. "This proof is strongly reminiscent of the type of reasoning required to solve a Sudoku puzzle, so we employ some Sudoku-like terminology in our argument to provide intuition and visual interest. A key step is to The shear transformation...then performs a 'tetris' move that eliminates constant rows to derive a secondary sudoku puzzle, which is then analyzed in turn. It is the iterations of this process that ultimately generate the aperiodic p-adic structure. "
In his blog post two months later, on November 29, Terence Tao wrote: "Greenfield and I have just uploaded the paper to arXiv. This is the full version of the results I published on this blog a few months ago... …this paper took a little longer than expected to complete due to a technical issue that required a workaround that we were unaware of at the time of the announcement.”
Terence Tao further explained that, as stated in the announcement, the initial strategy was to build a "tile language" - a language that could be used to encode "P-adic Sudoku puzzles"; Then show that if P is a sufficiently large prime, then the latter type of puzzle has only aperiodic solutions. "It turns out that the second half of the strategy succeeds." "During programming, we also found that once the two new definitions of 'expressible property' and 'weakly expressive property' were introduced, the coding part of the proof became more Modular and conceptual."
Terence Tao and Greenfield viewed their system of equations as a computer program: each line of code, or equation, is a command that, when combined, produces a program that achieves a specific goal.
Eventually, they find a target "tile" in a very high-dimensional space, not yet calculated in detail, but about 2^100^100 dimensional, a very complex, zigzag, full of holes.
Additionally, Tao says using their newly created "language" should create an undecidable puzzle. "(For example) there may be some tiles that we can never prove whether it will fill the space it is in."
Neither provable nor disprovable, mathematics is full of such "undecidable" statements. To prove that a statement is undecidable, mathematicians usually show that it is equivalent to another problem known to be undecidable. So, if the tiling problem turns out to be undecidable, it will serve as a new tool to prove the undecidability of many more problems.
Greenfield's resume shows that his research topic "translational tiling and orthogonal systems exponentials" (translational tiling and orthogonal systems exponentials) has received a grant of 117,056 from the National Science Foundation (NSF), the number is DMS-2242871, and the funding period is It is 2022 to 2025.
References:
1. https://www.quantamagazine.org/nasty-geometry-breaks-decades-old-tiling-conjecture-20221215/#newsletter
2. https://nautil.us/impossible-cookware-and-other-triumphs-of-the-penrose-tile-rp-234895/?_sp=1048d065-5002-434f-85c5-fa868cbccae2.1671370700212
3. https://huanqiukexue.com/a/qianyan/cailiao__huaxue/2017/0527/27301.html
4. https://terrytao.wordpress.com/2022/09/19/a-counterexample-to-the-periodic-tiling-conjecture/
5. https://arxiv.org/abs/1602.05738


