Ancient Greek philosophers believed that the world is composed of four basic elements, fire, air, water, and soil. In ancient my country, there was a similar idea, and the five elements were regarded as the origin of the world. The Platonic school also believed that there was a mysterious connection between the physical world and geometry, and knew that there were five types of regular polyhedra: the regular tetrahedron, the cube, the regular octahedron, the regular icosahedron, and the regular dodecahedron. 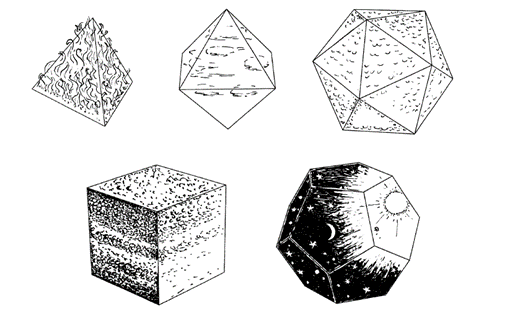
In these simple ideas, we see the importance of "classification". One manifestation of this ambition is the desire to have a comprehensive understanding of the world, and to classify objects according to their properties. Categorize, include everything in the world, and give them order.
The importance of classification in modern science continues unabated. The standard model of particles in physics, the periodic table of elements in the field of chemistry, and the categories, families and species of biology, etc., all embody the idea of "classification". "Classification" is also an important purpose of mathematical research. Mathematicians conduct research on the properties of mathematical objects and classify them according to their properties. As mathematician and math educator WW Sawyer said in his book Prelude to Mathematics: "Mathematics is the classification and study of all possible patterns" .
Professor Chen Xiuxiong and Professor Chen Gaoteren of the University of Science and Technology of China completed an important "classification" work. They proved that there are only four kinds of gravitational instantons. This is an important progress in the field of differential geometry, and papers have been published in journals such as Acta Mathematica, one of the four top mathematics journals in the world.
Acta Mathematica is regarded by many as the most prestigious academic journal in mathematics. In 2021, the "Acta Mathematica" will only publish 9 papers in the whole year, and in its 140-year history, in terms of the work unit at the time of publication, only about 10 papers have been published by Chinese university scholars. Acta Mathematica was founded in 1882 by Gösta Mittag-Leffler, a famous Swedish mathematician who made important contributions to the development of function theory. There are rumors that it is because of his emotional entanglement with Nobel that the Nobel Prize has not established a mathematics award, but there is no historical evidence to confirm this rumor. At the beginning of the establishment of "Acta Mathematica", many papers of mathematics masters were published. For example, two articles by Poincaré (1882) were published in the first issue. His more than 200 pages on the "Three-Body Problem" The famous paper (1890, regarded as the beginning of chaos theory) was also published on it.
So, what did Chinese scholars say about the work of gravitational instantons, and why did they appear in Acta Mathematica?
Instanton (instanton, not the familiar "Shunzi") is a concept in theoretical physics and mathematical physics.
Sunja. (Straits, pairs, threes with twos, bombs... poker is also a great "classification" study.)
Made a mistake, come back!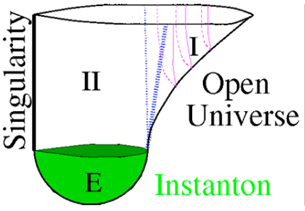
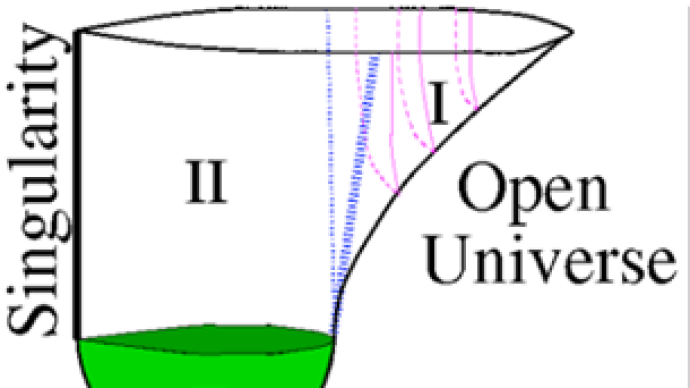
A kind of instanton: Hawking-Turok instanton. A "bubble" universe arises from Hawking-Turok instantons, where the vertical direction represents time and the horizontal direction represents space. (From the official website of the Cambridge University Centre for Theoretical Cosmology, founded by Hawking)
Mathematical models are proposed to describe and explain the natural world, and in some quantum mechanics and field theory models, a class of solutions to the equations of motion are called instantons. On the road of human beings to understand the composition of the world, instantons provide people with a perspective. In particle physics, for example, strong interactions in atomic nuclei are well described by quantum chromodynamics (QCD), and QCD instantons embody a fundamental non-perturbative property of Yang-Mills gauge theory. In addition, the study of instanton theory has gradually become an important direction of mathematics. For example, in the study of 4-dimensional instanton solutions of gauge theory, Simon Donaldson discovered a certain topological property of 4-dimensional manifolds - instanton invariants or Donaldson invariants, which can be used to solve 4-dimensional flows. shape to classify. Later, Donaldson won the Fields Medal for his work on the topological properties of 4-manifolds.
In 1977, Stephen Hawking proposed a new concept - "gravitational instanton". Hawking is the pioneer of quantum gravity theory, and his most well-known result, Hawking radiation, is the representative of the combination of gravity theory and quantum physics. Hawking's friend and Nobel Laureate in Physics, Roger Penrose, wrote in his obituary for Hawking: "Until the end of his life, Hawking has continued to study quantum gravity and related cosmological problems." The gravitational instanton was also proposed to unify quantum mechanics and Einstein's theory of gravity.
In general relativity, gravity is a manifestation of the properties of spacetime, which is described by a mathematical concept called a pseudo-Riemannian manifold. The so-called manifold is such an abstract mathematical space - any specific small area on it is similar to our ordinary space, that is, if there is a small life, it stands on the surface of the manifold and looks around. Go, it sees a "plane" around it. Gravitational instanton is also a manifold with special properties, it is a 4-dimensional complete Riemannian manifold that satisfies the vacuum Einstein equation. Through gravitational instantons, Hawking tried to combine the theory of gravity with the instanton theory in quantum physics to construct a quantum theory of gravity - Euclidean quantum gravity.
Gravitational instantons provide a new perspective on the quantization of gravity, and this unique mathematical structure has also aroused strong interest among mathematicians. How to construct the instanton model, many mathematics masters have carried out in-depth thinking.
In 1988, Atiyah (Michael Atiyah; 1966 Fields Medal, 2004 Abel Prize Laureate) and Nigel Hitchin (British Academy of Sciences, 2016 Shaw Laureate) were studied by Dirac magnetic monopoles Inspired by the idea, they collaborated to construct a class of examples of gravitational instantons.
There is a well-known problem in the field of graph theory called ADE classification. It was originally proposed by the great Russian mathematician Vladimir Arnold in the 1970s. He noticed that in various classification problems in different fields, there is a class of structures - Dynkin diagrams that often appear, and asked: Is there a general Could the theorem of fitness unify all these questions? Arnold once called ADE "a belief beyond mathematics"; others said, "If we were to engage with alien civilizations and show them how deep our civilization is, then the Dynkin diagram might be the best exhibit!" famously The Platonic polyhedron problem (that is, there are only 5 kinds of regular polyhedra) is one of the earliest examples of ADE classification. The ADE classification problem is deeply connected to the representation theory of Lie group Lie algebras. Using this known problem, in 1989, Peter Kronheimer (Peter Kronheimer; former chair of the mathematics department at Harvard University and winner of the Veblen Prize in 2007) constructed another class of examples of gravitational instantons.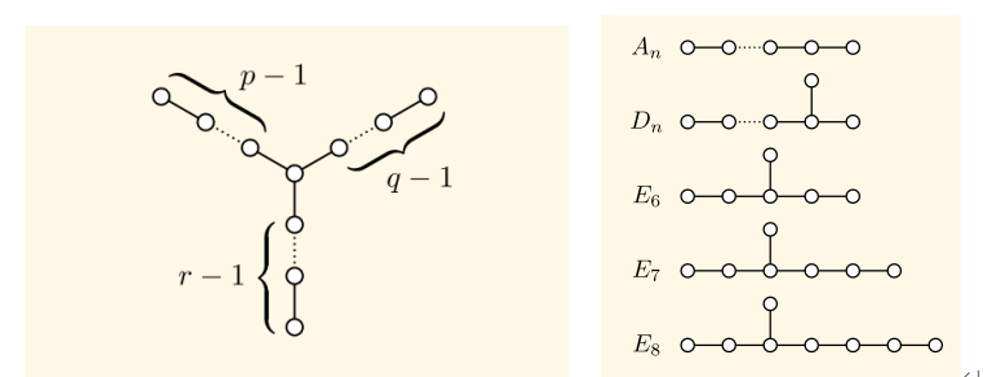
In 1977, Chengtong Yau (winner of the Fields Medal in 1982 and the Wolf Prize in Mathematics in 2010) proved the famous Calabi Conjecture. The general idea of Calabi's conjecture is to say, in a closed space, whether there is a gravitational field without matter distribution. In the 1980s, Qiu Chengtong and others extended the Calabi conjecture, pointing out that for open spaces, the Calabi conjecture can also be established under certain conditions. Mathematicians then construct models and work to achieve these conditions. In the process, in 1990, Qiu Chengtong and Tian Gang (academician of the Chinese Academy of Sciences, winner of the Veblen Prize in 1996) cooperated to construct two other types of examples of gravitational instantons.
In the years that followed, the mathematical community tried to construct new examples without success. In 2015, Chen Xiuxiong and Chen Gao cooperated and successfully proved that there are only these four types of gravitational instantons, and there is no other possibility! This achievement resulted in 3 papers. After a lengthy review, the core one will be published online in Acta Mathematica in 2022, and the other two have also been published in The Journal für die reine und angewandte Mathematik and Mathematica. Yearbook (Mathematische Annalen).


Xiuxiong Chen is the founding director and distinguished professor of the Geometry and Physics Research Center of USTC. He is an internationally renowned scholar in the fields of differential geometry and geometric analysis. In 2019, he won the Veblen Prize, the highest award in the world for differential geometry. Chen Gao, a student of Professor Chen Xiuxiong, was under the age of 21 when he completed this work. He is currently a special professor of the Geometry and Physics Research Center of USTC. In 2021, Chen Gao won the Green Orange Award and is the youngest winner of all previous years.
The Geometry and Physics Research Center led by Professor Chen Xiuxiong has a young and energetic team, and is striving to become a world-leading research platform in the fields of differential geometry, quantum field theory, algebraic geometry and topology. In the past few years, the research team has achieved a number of important achievements. The research results have been selected as the "Top Ten Science and Technology News in China" sponsored by Science and Technology Daily for two consecutive years and jointly selected by some academicians of the two academies and media.
(The original title of this article is "The "gravitational instanton" problem proposed by Hawking more than 40 years ago has been solved", published with the authorization of Surging Technology)

The ancient Greeks connected the four elements of Plato's regular polyhedron with fire, air, water, and earth, the basic elements that make up the material world, and gave the regular dodecahedron to the heavenly world: "God used the regular dodecahedron to organize the entire The constellations of the sky". (The picture comes from Penrose's "The Road to Reality")
In these simple ideas, we see the importance of "classification". One manifestation of this ambition is the desire to have a comprehensive understanding of the world, and to classify objects according to their properties. Categorize, include everything in the world, and give them order.
The importance of classification in modern science continues unabated. The standard model of particles in physics, the periodic table of elements in the field of chemistry, and the categories, families and species of biology, etc., all embody the idea of "classification". "Classification" is also an important purpose of mathematical research. Mathematicians conduct research on the properties of mathematical objects and classify them according to their properties. As mathematician and math educator WW Sawyer said in his book Prelude to Mathematics: "Mathematics is the classification and study of all possible patterns" .
Professor Chen Xiuxiong and Professor Chen Gaoteren of the University of Science and Technology of China completed an important "classification" work. They proved that there are only four kinds of gravitational instantons. This is an important progress in the field of differential geometry, and papers have been published in journals such as Acta Mathematica, one of the four top mathematics journals in the world.

Acta Mathematica's humble online page
Acta Mathematica is regarded by many as the most prestigious academic journal in mathematics. In 2021, the "Acta Mathematica" will only publish 9 papers in the whole year, and in its 140-year history, in terms of the work unit at the time of publication, only about 10 papers have been published by Chinese university scholars. Acta Mathematica was founded in 1882 by Gösta Mittag-Leffler, a famous Swedish mathematician who made important contributions to the development of function theory. There are rumors that it is because of his emotional entanglement with Nobel that the Nobel Prize has not established a mathematics award, but there is no historical evidence to confirm this rumor. At the beginning of the establishment of "Acta Mathematica", many papers of mathematics masters were published. For example, two articles by Poincaré (1882) were published in the first issue. His more than 200 pages on the "Three-Body Problem" The famous paper (1890, regarded as the beginning of chaos theory) was also published on it.
So, what did Chinese scholars say about the work of gravitational instantons, and why did they appear in Acta Mathematica?
Instanton (instanton, not the familiar "Shunzi") is a concept in theoretical physics and mathematical physics.

Sunja. (Straits, pairs, threes with twos, bombs... poker is also a great "classification" study.)
Made a mistake, come back!

A kind of instanton: Hawking-Turok instanton. A "bubble" universe arises from Hawking-Turok instantons, where the vertical direction represents time and the horizontal direction represents space. (From the official website of the Cambridge University Centre for Theoretical Cosmology, founded by Hawking)
Mathematical models are proposed to describe and explain the natural world, and in some quantum mechanics and field theory models, a class of solutions to the equations of motion are called instantons. On the road of human beings to understand the composition of the world, instantons provide people with a perspective. In particle physics, for example, strong interactions in atomic nuclei are well described by quantum chromodynamics (QCD), and QCD instantons embody a fundamental non-perturbative property of Yang-Mills gauge theory. In addition, the study of instanton theory has gradually become an important direction of mathematics. For example, in the study of 4-dimensional instanton solutions of gauge theory, Simon Donaldson discovered a certain topological property of 4-dimensional manifolds - instanton invariants or Donaldson invariants, which can be used to solve 4-dimensional flows. shape to classify. Later, Donaldson won the Fields Medal for his work on the topological properties of 4-manifolds.
In 1977, Stephen Hawking proposed a new concept - "gravitational instanton". Hawking is the pioneer of quantum gravity theory, and his most well-known result, Hawking radiation, is the representative of the combination of gravity theory and quantum physics. Hawking's friend and Nobel Laureate in Physics, Roger Penrose, wrote in his obituary for Hawking: "Until the end of his life, Hawking has continued to study quantum gravity and related cosmological problems." The gravitational instanton was also proposed to unify quantum mechanics and Einstein's theory of gravity.
In general relativity, gravity is a manifestation of the properties of spacetime, which is described by a mathematical concept called a pseudo-Riemannian manifold. The so-called manifold is such an abstract mathematical space - any specific small area on it is similar to our ordinary space, that is, if there is a small life, it stands on the surface of the manifold and looks around. Go, it sees a "plane" around it. Gravitational instanton is also a manifold with special properties, it is a 4-dimensional complete Riemannian manifold that satisfies the vacuum Einstein equation. Through gravitational instantons, Hawking tried to combine the theory of gravity with the instanton theory in quantum physics to construct a quantum theory of gravity - Euclidean quantum gravity.
Gravitational instantons provide a new perspective on the quantization of gravity, and this unique mathematical structure has also aroused strong interest among mathematicians. How to construct the instanton model, many mathematics masters have carried out in-depth thinking.
In 1988, Atiyah (Michael Atiyah; 1966 Fields Medal, 2004 Abel Prize Laureate) and Nigel Hitchin (British Academy of Sciences, 2016 Shaw Laureate) were studied by Dirac magnetic monopoles Inspired by the idea, they collaborated to construct a class of examples of gravitational instantons.
There is a well-known problem in the field of graph theory called ADE classification. It was originally proposed by the great Russian mathematician Vladimir Arnold in the 1970s. He noticed that in various classification problems in different fields, there is a class of structures - Dynkin diagrams that often appear, and asked: Is there a general Could the theorem of fitness unify all these questions? Arnold once called ADE "a belief beyond mathematics"; others said, "If we were to engage with alien civilizations and show them how deep our civilization is, then the Dynkin diagram might be the best exhibit!" famously The Platonic polyhedron problem (that is, there are only 5 kinds of regular polyhedra) is one of the earliest examples of ADE classification. The ADE classification problem is deeply connected to the representation theory of Lie group Lie algebras. Using this known problem, in 1989, Peter Kronheimer (Peter Kronheimer; former chair of the mathematics department at Harvard University and winner of the Veblen Prize in 2007) constructed another class of examples of gravitational instantons.

Dynkin diagram. For the ternary tree structure shown on the left, 1/p+1/q+1/r>1 is required, where p, q, r are positive integers. There are only 5 categories of answers (right).
In 1977, Chengtong Yau (winner of the Fields Medal in 1982 and the Wolf Prize in Mathematics in 2010) proved the famous Calabi Conjecture. The general idea of Calabi's conjecture is to say, in a closed space, whether there is a gravitational field without matter distribution. In the 1980s, Qiu Chengtong and others extended the Calabi conjecture, pointing out that for open spaces, the Calabi conjecture can also be established under certain conditions. Mathematicians then construct models and work to achieve these conditions. In the process, in 1990, Qiu Chengtong and Tian Gang (academician of the Chinese Academy of Sciences, winner of the Veblen Prize in 1996) cooperated to construct two other types of examples of gravitational instantons.
In the years that followed, the mathematical community tried to construct new examples without success. In 2015, Chen Xiuxiong and Chen Gao cooperated and successfully proved that there are only these four types of gravitational instantons, and there is no other possibility! This achievement resulted in 3 papers. After a lengthy review, the core one will be published online in Acta Mathematica in 2022, and the other two have also been published in The Journal für die reine und angewandte Mathematik and Mathematica. Yearbook (Mathematische Annalen).



Xiuxiong Chen is the founding director and distinguished professor of the Geometry and Physics Research Center of USTC. He is an internationally renowned scholar in the fields of differential geometry and geometric analysis. In 2019, he won the Veblen Prize, the highest award in the world for differential geometry. Chen Gao, a student of Professor Chen Xiuxiong, was under the age of 21 when he completed this work. He is currently a special professor of the Geometry and Physics Research Center of USTC. In 2021, Chen Gao won the Green Orange Award and is the youngest winner of all previous years.
The Geometry and Physics Research Center led by Professor Chen Xiuxiong has a young and energetic team, and is striving to become a world-leading research platform in the fields of differential geometry, quantum field theory, algebraic geometry and topology. In the past few years, the research team has achieved a number of important achievements. The research results have been selected as the "Top Ten Science and Technology News in China" sponsored by Science and Technology Daily for two consecutive years and jointly selected by some academicians of the two academies and media.
(The original title of this article is "The "gravitational instanton" problem proposed by Hawking more than 40 years ago has been solved", published with the authorization of Surging Technology)
Related Posts
0 Comments
Write A Comments