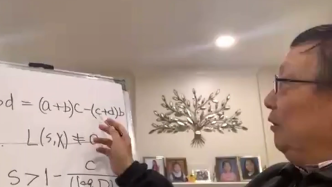
"The question is, which (number-theoretic) universe do we live in?"

One has zero and one has no zero.

Before Chinese-American mathematician and UC Santa Barbara professor Yitang Zhang published his latest research paper on the Landau-Siegel zeros conjecture, the zeros divided number theory into the above two universes.

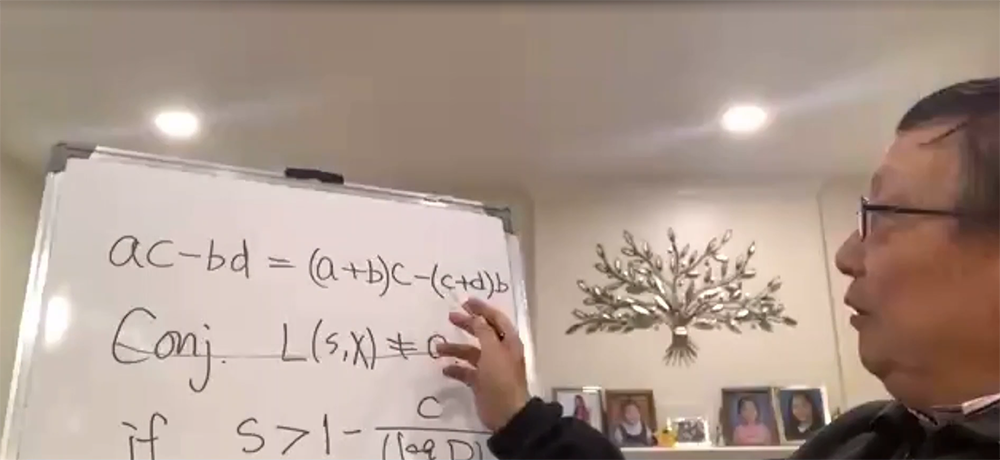
Professor Zhang Yitang gave a speech on the Landau-Siegel zero-point conjecture to teachers, students and the public at Peking University on the morning of November 8

Because they don't know whether this zero exists or not, number theorists have to discuss two situations: If this zero exists, what conclusions can be drawn? If it didn't exist, what would be the conclusion?

In his speech to the teachers and students of Shandong University three days ago and to the teachers and students of Peking University and the public on the morning of November 8, Professor Zhang Yitang repeatedly mentioned the proof of Landau-Siegel's zero-point conjecture in his latest paper. Innovative ideas or "New idea".

He also said that his paper still needs to be revised and supplemented, and more importantly, to be simplified. The new research results will give a very strong result on the class number problem of quadratic fields in algebraic number theory.

Professor Zhang Yitang also mentioned "finding a needle in a haystack" again in his speech. Compared to his 2013 research breakthrough on the twin prime conjecture, proving the Landau-Siegel conjecture is the real needle in a haystack, he said.

On the morning of November 8, for the "New idea" (new method) that Zhang Yitang mentioned in his speech to prove the Landau-Siegel zero-point conjecture, a postdoctoral fellow from the School of Mathematical Sciences of Peking University who listened to the whole lecture told The Paper ( www.thepaper.cn) explained that, most briefly, he replaced the z(n) sequence in the calculation with a(n), b(n), c(n), d(n) sequence , and then use the Cauchy inequality to deduce the contradiction, proving that there is no Landau-Siegel zero in a specific range.

The postdoctoral fellow further explained that, specifically, Professor Zhang Yitang gave an example in his speech. For a real continuous function, the function values between two consecutive zeros have the same sign. In this way, it is necessary to prove that the zero is at a certain point. Local existence is equivalent to proving that the product of the function values of the two local endpoints is not positive. If a sequence x(n) is constructed to describe the positive and negative characteristics of the zero point, then proving that a certain item in x(n) is negative means that the zero point is zero. exist. Similarly, the Dirichlet L function (when the feature is trivial, that is, the Riemann zeta function) considering the real primitive features, its zeros exist, and it is also necessary to prove that for a certain sequence x(n), one of them is negative. The traditional method is to take a set of real z(n) and consider the summation of x(n)(z(n))^2. If it is negative, then there must be a negative item in x(n). But traditional methods cannot break from an infinitesimal ε (epsilon) to 0. Professor Zhang Yitang's method is to use a(n), b(n), c(n), and d(n) to do two sets of summations and approximate them at the same time; then use Cauchy's inequality to deduce the magnitude relationship. The value of this work is to improve the lower bound of L(1,χ) from the negative ε power of D, which is not effective, to the negative constant power of log D, which is effective.

In the question-and-answer session after the speech, someone asked whether the new idea you introduced was "primary" and was actually extracted from very deep work, or was it directly used after finding a needle in a haystack Got an elementary idea to guide the work?

When answering this question, Zhang Yitang said, " Of course, my thesis still needs to be revised and supplemented a lot. Perhaps more importantly, it should be simplified. Otherwise, it will indeed be a headache."

On November 6, Fields Medal winner James Maynard (James Maynard) was his Ph.D. tutor, British mathematician dedicated to the field of analytic number theory, and retired professor at the Institute of Mathematics at Oxford University Roger Heath-Brown ( Roger Heath-Brown FRS) told The Paper, "It takes a long time to study this paper (Zhang Yitang's), so I can't say whether it's correct yet. But it's clearly written and strategically wise."

Zhang Yitang said in his speech, "Sometimes you say that you use some advanced things, but in fact, in terms of scope, it does not exceed the scope of complex variable functions, but it has its special processing method. Some things are made It is very delicate, very delicate, so it is a whole set (methods). Just like in my paper, there are actually many (such special processing methods). Finally , I may have to fill in the details later. There are some arithmetic, There are some special 'and', I can know the result (of), basically I will give a statement. But many details, now speaking, writing these things, it is still a headache for me ."

Zhang Yitang said, "Strictly speaking, each step should be said to be elementary, but the real choice of z(n), and in the end, if you want to be able to calculate the sum, you need to use a lot of analytical tools."

He also cited Fields Medal winner Selberg's research as an example, saying, " Sometimes elementary is harder and more challenging than parsing stuff. "

Others asked, what applications would the breakthroughs in the Landau-Siegel conjecture have in number theory or arithmetic geometry?

Zhang Yitang replied that in number theory, it solves at least one unsolved problem - "the distribution of prime numbers in arithmetic progressions". "(If) there may be a Landau-Siegel zero, then in some arithmetic series, there will be very many prime numbers; in some, there will be very few prime numbers. After my results come out, at least this question will be put to rest. solved."

Zhang Yitang said, "In the application, because it involves analytic number theory, this (result) must be used everywhere." "There is also a problem of the class number of the quadratic field in algebraic number theory, which will give a very A strong result. ”

Three preprint papers published by Yitang Zhang on the website arXiv

Zhang Yitang published "Bounded Intervals between Prime Numbers" in Annals of Mathematics on April 17, 2013, and proved for the first time that there are infinitely many pairs of prime numbers (p, q), where the difference between each pair of prime numbers , that is, the distance between p and q, not more than 70 million. This has made breakthrough work for the solution of the century problem "twin prime conjecture", and he has risen from an obscure university lecturer to the ranks of the world's heavyweight mathematicians. Subsequently, the number "70 million" was improved to 600 and 246 by peers in the mathematics community.

On May 29, 2007, Zhang Yitang submitted a paper titled "On the Landau-Siegel Zeros Conjecture" on the preprint website arXiv. The paper has a total of 54 pages and 13 sections in the main text. "We provide a proof of a variant of the Landau-Siegel zero-point conjecture," the paper said.

Fifteen years later, Zhang Yitang republished his paper on the Landau-Siegel zero-point conjecture. Two days after the internal outflow, on November 7, 2022, its latest paper was officially released on the preprint website arXiv. The title of the paper is Discrete mean estimates and the Landau-Siegel Zero. The full text is 111 pages, with 18 sections in the text.

At 11:05 a.m. on November 6th, Shandong University WeChat public account released Lu Guangshi, a professor and doctoral supervisor of the School of Mathematics of Shandong University, the former deputy dean of the School of Mathematics, and the executive dean of the Australian National Union College of Science of Shandong University, and data science research of Shandong University. An article co-authored by Huang Bingrong, a professor of the School of Medicine and a doctoral supervisor, and others.

According to the article, Professor Zhang Yitang introduced his innovative ideas in the research of the Landau-Siegel zero-point conjecture, and proved in his latest preprint paper that the real feature L-function of modulo D is in the interval (1−c( log D)^−2024,1] has no real zeros.

" If you replace 2024 here with 1, you will get the Landau-Siegel zero-point conjecture in its original form. Although 2024 is greater than 1, it is not substantially different from 1 in the mathematical sense." Shandong University WeChat public account The above article said.

More than 20 days ago, at the event of the Peking University Greater New York Area Alumni Association held at 8:00 pm on October 14th Eastern Time (8:00 am on October 15th, Beijing time), Zhang Yitang announced in advance that Landau-West had been resolved. News on the problem of Geer's zero-point conjecture. To solve this problem, he said, it boils down to making an inequality; that is, to construct a set of numbers. "Some people say that the twin prime conjecture is a needle in a haystack. In fact, Landau-Siegel zero is a needle in a haystack. Over the years, I have tried countless (situations), and the numbers have been substituted into it. I have established a whole set of formulas, so I can calculate. I've tried countless situations, and each time it's one ε (sound: ipsilon)."

He said that he searched the "bottom of the sea" and finally found that this zero-point conjecture can be solved without the needle. "I'm pretty sure I did it. I know I did it right."

In his speech on the morning of November 8, Zhang Yitang said that, in essence, he had proved the Landau-Siegel zero-point conjecture. Just like his previous results on the twin prime conjecture, the results can be improved. This latest research breakthrough will have many applications and lead to many theorems.

In other words, Yitang Zhang's latest paper shows that, within a certain range, the Landau-Siegel zero does not exist. In this case, the Landau-Siegel zero-point conjecture is correct or true.

The "Landau-Siegel zero" is defined as a counterexample to the generalized Riemann conjecture. A conjecture that asserts that the "Landau-Siegel zero" does not exist is called the Landau-Siegel zero conjecture.

Zhang Yitang also said in his speech that he has achieved 2024 on the relevant index of the proof of Landau-Siegel's zero-point conjecture, "I'm glad." This result can be improved, but to what extent can the index 2024 be improved? "I think I can get at least a few hundred. But getting 1? I'm still not enough."

This latest achievement of Professor Zhang Yitang has aroused great concern in the mathematics community and the public. Will this be another important breakthrough in his mathematical research? To be confirmed by experts in the mathematics community.