
· "The relocation of the center of mathematics development in history is basically consistent with the relocation of social, political and economic centers of gravity." If more people from all walks of life love mathematics in the future, and enjoy mathematics discussion and research, then our country will be must be very strong in mathematics.
Part 1: Mathematical Power and Its Enlightenment
1. From the ICM to see the mathematics power
How to see which mathematical powers are today, a reference standard is the Fields Medal award.
The quadrennial International Congress of Mathematicians (ICM) has officially ended. This year, France, the United States, the United Kingdom, and Ukraine each won the Fields Medal. How well a country wins a Fields Medal is a good indicator of its mathematical prowess. 
Figure 1: 2022 Fields Medal winners (from left to right): Hugo Duminil-Copin, Xu Xianer, James Maynard, Maryna Viazovska
Source: ICM official website/Matteo Fieni/Lance Murphey/Ryan Cowan/Matteo Fieni
From the perspective of nationality, the nationality-number bar chart of Fields Medal winners is as follows. The blue represents the total number of winners, and the dark red represents the number of foreigners. It is not difficult to see from the picture that the top four are: 19 from the United States, 13 from France, 8 from the United Kingdom, and 5 from Russia; the United States, France, the United Kingdom, and Russia account for "most of the country" in terms of numbers; if Russia and the Soviet Union are taken as A "Pan-Russian region" with a total of 8 people. As for France and Germany, which were once the centers of mathematics in the world, France is still strong, and Germany seems to be in decline. 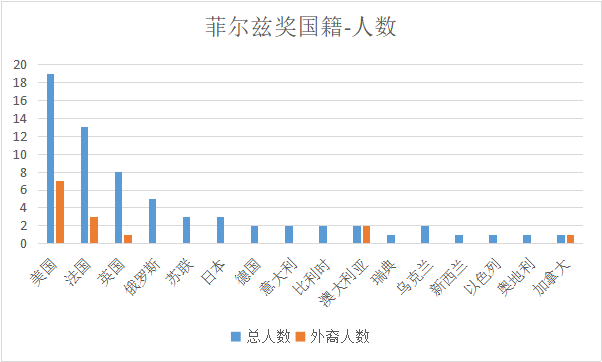
Figure 2: Statistics of previous Fields Medals (1936-2022)
The original purpose of Fields' establishment of the Fields Medal was to promote the development of mathematics in North America. Because of historical reasons, the rise of mathematics in the United States after World War II, and the decline of Germany. It is not difficult to find from the picture that the United States, France, and the United Kingdom are the top three and also the countries with the most awards for foreigners. Mainly because of the massacre and defeat of Germany in the early days, which led to brain drain; the disintegration of the Soviet Union, which led to brain drain; and the brain drain from underdeveloped and unstable countries and regions. Most of this talent went to the US, France and the UK. Why can the United States, France, Britain, Russia, and Germany become mathematical powers? We can find answers in history.
2. Historical Migration of Mathematical Centers
Academician Zhang Gongqing said, "Mathematical strength often affects national strength, and a world power must be a mathematical power". Professor Li Wenlin also said, "The relocation of the center of mathematics development in history is basically consistent with the relocation of the social, political and economic centers of gravity"[1]. 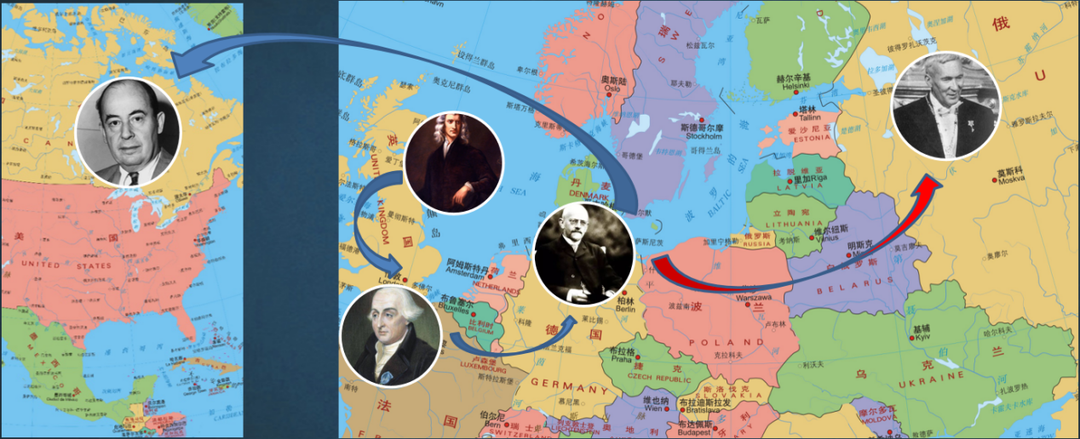
Figure 3: Migration of mathematically developed centers in the history of modern mathematics
From the fifteenth century the center of mathematical activity moved back to Europe due to the rise of capitalism, and shifted between different countries within Europe as the center of gravity of the bourgeois revolution shifted:
The bourgeois revolution in England brought its maritime hegemony, and at the same time created the birth of the Newtonian School and the Royal Society;
·Through the French Revolution in the 18th century, French mathematics replaced Britain and took the top spot in Europe, and Paris became a veritable "hive of mathematical activities" for a long time;
·France maintained its mathematical superiority until the late 19th century. After the 1970s, Germany's unification movement made German mathematics rise to the top, and finally Göttingen became the "Mecca" that mathematicians all over the world yearned for;
·The golden age of German mathematicians was devastated by Hitler's fascist catastrophe. After World War II, the United States became a paradise for Western mathematicians.
·The development of mathematics in the Soviet Union was very strong before and after World War II. In the 20th century, hundreds of mathematicians were cultivated, and Moscow University became the cradle of mathematicians.
In general, the development of mathematics met the needs of the political, economic, and military development of the capitalist system at that time. Politically, when Europe went through a long and dark Middle Ages, the development of mathematics not only promoted the progress of natural science, but also acted as a revolutionary driving force. The establishment and consolidation of the capitalist system; Economically, due to the successive industrial revolutions carried out in various bourgeois countries, the development of mathematics also directly or indirectly promoted the development of productive forces at that time; Military, the unbalanced development of Western European countries aggravated the interests of countries Wars caused by contradictions, coupled with overseas colonization, required vigorous development of mathematics to meet military needs. The same applies here to the socialist system of the Soviet Union.
3. Attach great importance to university mathematics education and personnel training
(1) Germany - University of Göttingen
The University of Göttingen has almost trained mathematicians around the world. And Klein is the actual helm of the University of Göttingen and a handsome mathematician.
Klein's reputation attracts students from all over the world, especially the United States. A young Englishman wrote to a friend in Cambridge about the mathematics department in Göttingen: "We have a very mixed nationality here, five Americans, one Swiss French, one Hungarian, one Italian, and a few others. One has German ancestry." [2] The following mainly talks about Klein's mathematics education from three aspects.
Pay attention to teaching
teach. Klein taught extremely well and was a good example for teachers to learn from. The lecture notes he wrote are not only fluent and clear, but also well-structured, which is very attractive to readers. Before class, he always made full preparations. At the same time, he processed and revised the parts of the speech that were unclear and lacked in expression, and made careful arrangements for the content of the textbook, mathematical formulas, charts and citations, so as to be well-conceived and meticulous.
When Klein lectures, his thoughts are clear and the key points are highlighted. He believes that students should think and analyze by themselves to complete the proof of the theorem. In order for students to master all the content taught in class, they also need to seriously review, read reference books and complete homework after class, which often takes several times more time. His teaching method effectively cultivates students' self-learning ability and ability to analyze and solve problems.
Klein is very particular about writing on the blackboard. He never erased the writing on the blackboard during the lecture, and finally formed a complete summary of the lecture content. He writes every question in a proper, well-organized manner, giving people a sense of beauty.
Focus on seminars. Klein attaches great importance to the teaching method of seminars. He believes that this method can cultivate students' conscious learning ability and stimulate students' interest in academic research. He often brings the problems he is researching to the discussion class, and at the same time introduces the ideas to solve the problems to the students; sometimes he also asks the students to explain the works they have learned on the blackboard, and then asks everyone to ask questions for discussion.
walk. Matters big and small in the math department are tackled every Thursday at 3pm math walks. These walks are informal classes that are available to both faculty and students in the department. During the walk, I mainly talked about math problems, and of course also included some other affairs in the department.
teacher request. Klein also believed that teachers should have a higher mathematical point of view, and he believed that it was necessary to talk about the history of mathematics in mathematics.
recruit talents
He recruited talents and established a strong team of mathematics professors, such as Hilbert, Minkowski, Nott, Weyl and others, and revitalized the Göttingen School of Mathematics.
mathematics teaching reform
He vigorously promoted the reform of mathematics teaching, paying equal attention to basic mathematics and applied mathematics, and extended the teaching reform to all of Germany, cultivating a large number of talents who are both scientific and technological, have a profound vision and can solve practical problems. He also vigorously advocated applied mathematics and founded the Göttingen School of Applied Mathematics. As a result, Göttingen was soon at the forefront of the world in applied mathematics research. Later, some countries followed suit and followed suit. At the same time, he worked hard to promote the application of mathematics, mechanics and other basic disciplines in engineering technology, and established the Department of Applied Mechanics at the University of Göttingen to promote the development of applied mechanics. Klein's discerning eyes and pearls brought in Prandtl, and the Göttingen School of Applied Mechanics has been carried forward since then.
(2) Russia - Moscow University
Russian mathematics began to rise in the 19th century, and in the 20th century, it became one of the world's mathematical powers during the former Soviet Union. In particular, the Soviet Union successfully launched the first artificial earth satellite in 1958, which shocked the world. At the time, U.S. President John F. Kennedy was determined to overtake the Soviet Union in space technology. He learned that: one of the reasons why the Soviet Union successfully launched satellites is that the Soviet Union is in a leading position in the field of mathematics related to this; in addition, the Soviet Union attaches great importance to basic science education (including mathematics education) and it also has strong strength in basic scientific research an important reason. So Kennedy ordered the development of mathematics.
Most of the papers of Soviet scientists were published in Russian. The American Mathematical Society and the London Mathematical Society joined forces to translate almost all the well-known comprehensive mathematics journals in Russia and many professional mathematics journals into English word for word. A large number of Soviet textbooks have been translated into English and other languages and distributed and applied all over the world, which also shows people's recognition of the education and scientific research system of the former Soviet Union. To this day, many excellent mathematics training institutions in the United States refer to the system of the former Soviet Union.
Throughout the history of mathematics in the 20th century, Soviet-Russian mathematics is undoubtedly a remarkable force. Over the past century, hundreds of world-class mathematicians have emerged in Soviet Russia, and most of these outstanding mathematicians graduated from Moscow University.
Master-Apprentice Tradition: Yegolov-Lukin-Kolmogorov-Gervander
The biggest achievement of the Yegolov seminar was the achievement of mathematician Lukin. This person is the kind of person who connects the past and the future. He is also a master of real analysis. He has written some classic textbooks and trained many masters at the same time. The famous Kolmogorov is one of them. In the era of Kolmogorov, the Moscow School reached its peak. 
Figure 4: Kolmogorov
Kolmogorov was a great teacher who influenced countless mathematicians. The number of students directly under his guidance is also staggering, perhaps an insurmountable record: 67. Among them, 14 became academicians of the Soviet Academy of Sciences.
In 1932, Gelfand, who had not finished high school and had not attended university, was admitted as a graduate student by Moscow University, under the tutelage of Kolmogorov. 
Figure 5: Gail van der
From 1943, Gelfand organized his own seminar on mathematics at Moscow University. He set up the seminar as a center for selecting collaborators and cultivating rookies in mathematics, and eventually the seminar developed into the world-famous "Gelvander Mathematics Seminar", which lasted until Gelfandre immigrated to the United States in 1990. Since then, he has brought the tradition of seminars to Rutgers University.
Advanced seminar
The holding of open seminars on advanced mathematics has played a key role, as is the norm at Moscow State University. Open to everyone—from talented high school students to academics barred from official institutions, these seminars foster intergenerational and inter-institutional connections and bring people together. The largest and most prestigious of these public seminars is the Gelfand Seminar. In the memoirs of many scholars, "about two or three hundred people must have attended" when they recorded the grand occasion.
4. Looking at the whole country: paying great attention to mathematics education in primary and secondary schools
Here, Klein of Germany and Kolmogorov of Russia are the main representatives.
(1) Germany - Klein
Organize scientific education reform and popularize mathematics knowledge. Klein personally participated in the development, improvement and expansion of German secondary school science education plans; promoted first-class mathematicians to give popular lectures to non-mathematical experts; organized and compiled a thirty-volume mathematical dictionary to improve the level of science and mathematics in the whole society.
Klein's main works include "Advanced Geometry", "Non-Euclidean Geometry", "Elementary Mathematics from a High Viewpoint", "Lectures on the Development of Mathematics in the 19th Century" and so on. In addition, there are papers such as "The Theory of Algebraic Functions on Riemannian Geometry", "Lectures on the Icosahedron", and "Lectures on the Theory of Automorphic Functions". What is especially commendable is the thirty-volume mathematical dictionary he compiled, which has brought great convenience to mathematics educators.
(2) Russia - Kolmogorov
Kolmogorov has always attached great importance to mathematics education. In order to cultivate outstanding young mathematical talents, he opened a boarding school for mathematics and physics (known as the Kolmogorov School). In his later years, he engaged in the reform of mathematics education in secondary schools, trying to improve the level of mathematics education in the entire Soviet Union. He held seminars, compiled textbooks, organized experiments, and taught geometry classes in middle schools in person, all of which cost him a lot of effort.
We can think about a question, why are there so many young mathematicians in foreign countries? It is that it has developed a mathematical culture for a long time. Most people of a nation know what mathematics is about since childhood, and if they ponder and understand mathematics, they will be able to produce results earlier and become mathematicians.
Part II: Vision: Mathematical Culture in China in the Future
Today, Mr. Li Hongling from Suqian College quoted Gu Pei's definition of "mathematical culture" in his lecture, which was very enlightening. Mathematical culture includes not only the thought, spirit, method, point of view, language of mathematics, as well as their formation and development, but also mathematicians, mathematics history, mathematics beauty, mathematics education, the human element in mathematics development, the connection between mathematics and society, The relationship between mathematics and various cultures, etc.
Here, I want to interpret mathematical culture from another angle. I think we also need to pay attention to whether the country or society has a cultural environment that is conducive to the development of mathematics. For example, we all know that Brazil has a strong football culture, not only because they play football well, but also because of the football atmosphere. In Brazil, football has truly become a national sport. Football can be seen everywhere in the streets of Brazil, whether in cities or in slums. At present, the popularity of mahjong and chess in our country is quite high. You can always see chess games and onlookers in the streets and alleys, but there are too few people in our country who are interested in mathematics. If one day, we can find a few old ladies on the street who can talk about mathematics, then we will definitely be able to build a math powerhouse.
Next, I mainly talk about the vision of the future Chinese mathematics culture from five aspects.
1. Mathematicians and researchers pay more attention to mathematics education
Mathematicians can also be mathematics educators, and mathematics education includes mathematics education in universities, mathematics education in primary and secondary schools, and mathematics popularization education for the whole society. Since ancient times, many mathematicians have put mathematics education in an important position. At the beginning of the 20th century, the German mathematician Klein advocated the reform movement of mathematics education based on "function as the key". The American mathematician Moore advocated mixed mathematics, the Japanese mathematicians Kunihiko Kodaira and Hironaka Heisuke criticized the "New Number Movement" in the 1960s, and my country's Hua Luogeng and others were concerned about mathematics education... These historical cases demonstrate the relationship between mathematicians and mathematicians close relationship with mathematics education. Because of their special status, mathematicians play a vital role in the development of mathematics education.
After the founding of New China, there was an era of "elite teaching materials". Many famous experts, scholars, and professors compiled teaching materials, and even super experts like Hua Luogeng led teams to compile mathematics teaching materials for primary and secondary schools. In recent years, many scholars in my country have paid attention to and participated in the reform of mathematics education and the formulation of mathematics curriculum standards. For example, Academician Zhang Jingzhong's "From Mathematics Education to Educational Mathematics", Academician Wang Zikun and Professor Xu Lizhi's "MM Education Method" (using the viewpoint of mathematical methodology to guide mathematics teaching), and Academician Yuan Yaxiang vigorously promote the work of mathematics popularization education. Their focus on math education has cheered math educators. At present, at the level of mathematics popularization, there are not many better popular science platforms. The popular science of the WeChat public account of the Institute of Physics of the Chinese Academy of Sciences is well done, combined with reality and contains rich physical knowledge, which is worthy of reference in the field of mathematics.
It is hoped that more mathematics will pay attention to mathematics education in the future, have a deeper understanding of the development of mathematics, the laws and order of mathematics learning, and use it to guide students. This will help to cultivate mathematically literate students and improve the research level of the entire mathematical field.
2. Mathematical popular science works have more types and higher quality
At present, the number of mathematical popular science books published in my country has been considerable, but there is still a lot of room for improvement in other aspects. For example, the volume is not small, but the scope of influence is limited, and the primary and secondary school students in the county and township are rarely contacted; the content focuses on elementary mathematics, while the popular science on advanced mathematics is small, and the audience is narrow; there is also a lack of young and promising mathematics popular science writers. 
Figure 6: Core authors of mathematical popular science who have published more than 10 books
Source: "Research on the Development of Mathematical Popular Science Books Since the Founding of New China: Analysis Based on Series" 2021
We are in great need of young mathematics popularization writers now. Of course, many teachers participating in the conference have a lot of excellent works, and we hope that more mathematics popularization creative talents will emerge in the future.
3. Mathematical societies in colleges and universities are flourishing
Many colleges and universities in Beijing have math clubs. I think math clubs can play a very important role in improving students' interest in mathematics, understanding the history of mathematics, and learning mathematical ideas. In my opinion, the activities of a good mathematics club can mainly include the following four aspects: daily Q&A, pre-exam tutoring, competition training, etc.; holding large-scale mathematics lectures; visiting old mathematics professors; organizing learning and discussing mathematical ideas and mathematics history.
I had 3 years of club experience during my undergraduate years. At that time, the club established a mathematics exchange group with a scale of nearly 2,000 every year, which not only answered mathematics questions for all students in the school, but also established a group of advanced mathematics lecturers among the students to review and answer questions for exams. Our society also invited Professor Li Shangzhi, Academician Lin Qun and Academician Yan Jiaan to give lectures at the school, which is an advantage of the university platform. In addition, the club also organizes members to study and discuss mathematical popular science every week, such as "Introduction to the History of Mathematics" and "The History of Calculus".
Today, our "Mathematics Jingwei.com" has also cooperated with many school mathematics clubs to host lectures, and promoted the courses of some famous teachers from famous schools to other schools and the majority of netizens. Mathematical societies in colleges and universities are a very good practical platform for disseminating mathematics culture, and we also hope that in the future, mathematical societies in colleges and universities can flourish.
4. The public understand mathematics, love mathematics, and study mathematics
Many people in our country are keen to talk about Chen Jingrun's "1+2" when talking about mathematical research, but few people understand its specific meaning. On the one hand, it reflects the great influence of the reportage "Goldbach Conjecture" more than 40 years ago, and on the other hand, it also reflects the insufficient popularity of mathematical ideas corresponding to the publicity of mathematical achievements. 
Figure 7: Xu Chi's Goldbach Conjecture (left), Goldbach's letter to Euler in 1742 (right)
Our country has entered into the era of "National Mathematics Olympiad". This year is the 23rd time that the Chinese team has won the world first in the International Mathematical Olympiad (IMO). Since China participated in the Olympic Games for the first time in 1985, in the past 30 years, Chinese competitors have won a total of 174 gold medals, and the average number of gold medals that can be won in a single competition is 4.7. These figures are the first in the world. However, there are no Fields Medal winners. It can be said that there are many students who are talented in mathematics in China, but whether these students love mathematics from the bottom of their hearts, are full of fun in mathematics research, and how far they can go on the road of mathematics in the future is a question worthy of in-depth thinking in the mathematics education community. . 
Figure 8: The Era of National Mathematics Olympiad
In the streets and alleys of China, wherever there is a chess game, there must be onlookers, and everyone likes to ponder and discuss. In the UK, there is a phenomenon where the unassuming grandmother also discusses math problems. We had a face-to-face exchange with Mr. Li Wenlin from the Institute of Mathematics and Systems Science of the Chinese Academy of Sciences before. He talked about an old lady he met in a British coffee shop. He heard that he was studying mathematics and was very excited. He chatted with him about himself. The scene of learning mathematics in high school. In the morning report, Academician Tian Gang introduced a housewife, Marjorie, to solve the problem of pentagon dense tiling. When the headquarters of the American Mathematical Society was renovated, the new floor used the pentagon cladding discovered by Marjorie. It can be seen that mathematics is also a very "down-to-earth" science abroad, and ordinary people other than mathematicians are also willing to discuss and study it.
5. The future can be expected: the relevant policies of mathematics cultural education
The future is promising. In the past 20 years, our government has successively issued relevant policies on mathematics cultural education, which is enough to show that the country attaches great importance to mathematics cultural education.
In June 2002, my country officially promulgated the "Law of the People's Republic of China on Popularization of Science and Technology", which is the only national law in the world that specifically targets popular science.
In March 2006, my country issued and implemented the "Outline of Action Plan for National Science Literacy (2006-2010-2020)", which is the first programmatic document on improving the scientific literacy of the whole people since the founding of the People's Republic of China.
my country established the Mathematics Education Branch of the Chinese Mathematical Society in July 2021.
In order to strengthen the guidance of mathematics popularization work, my country has established the Mathematics Education Branch of the Chinese Mathematical Society in July 2021. On February 25, 2022, the China Association for Science and Technology released the "Key Points of Science Popularization Work of the China Association for Science and Technology in 2022", in which it proposed to build a grassroots science popularization organization mobilization system linked by "provincial, municipal and county civilized practice centers". The establishment of the mathematics education branch and the establishment of the mobilization system for grass-roots popular science organizations show the country's determination and action to improve the scientific literacy of the whole people, especially the mathematical literacy. of great significance.
Fundamental math research requires little or no expensive instruments, just a brain and pen and paper. In the future, if more people from all walks of life love mathematics and enjoy discussing and researching mathematics, then our country's mathematical strength must be very strong.
references:
[1] Li Wenlin. Introduction to the History of Mathematics (Fourth Edition) [M]. Beijing: Higher Education Press, 2021.
[2] Zhang Dianzhou. The latitude and longitude of mathematics in the 20th century [M]. Shanghai: East China Normal University Press, 2002.
(The author Wang Yongtao, a PhD student in mathematics at Beihang University, has established a "mathematics latitude and longitude network" with his colleagues during college. This article is the 11th session of the Chinese Mathematical Society held by Wang Yongtao in Kaifeng, Henan in July 2022 The report made at the National Mathematical Culture Forum, the original title is "A Mathematical Power in the View of Mathematical Culture". "Pengpai Technology" was published with the authorization of Mathematical Jingwei Network, with slight deletions.)